AI Lab 5

BFS Questions

Implement Breadth-First Search

Write a Python function `bfs(graph, start_node)` that performs a Breadth-First Search on a given graph. The graph is represented as an adjacency list (a dictionary where keys are nodes and values are lists of their neighbors). The function should return a list of nodes in the order they were visited.

Visual Example:

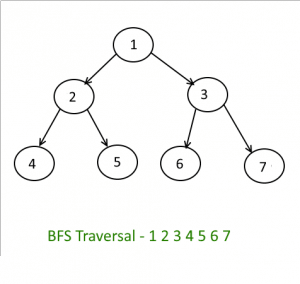
Simple undirected graph for traversal examples

# For the graph above:
graph = {
  'A': ['B', 'C'], 'B': ['A', 'D', 'E'],
  'C': ['A', 'F'], 'D': ['B'],
  'E': ['B', 'F'], 'F': ['C', 'E']
}
# Starting at node 'A'
Input: graph, 'A'
Output: ['A', 'B', 'C', 'D', 'E', 'F']

The traversal explores level by level: A, then B and C, then D, E, and F.

Shortest Path in a Grid

You are given an `n x n` binary grid. A `0` represents an open path, and a `1` represents an obstacle. Find the length of the shortest clear path from the top-left cell `(0, 0)` to the bottom-right cell `(n-1, n-1)`. A clear path can move in 8 directions (horizontally, vertically, and diagonally). If no such path exists, return -1.

Example:

Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

DFS Questions

Implement Depth-First Search

Write a Python function `dfs(graph, start_node)` that performs a Depth-First Search on a given graph. The graph is represented as an adjacency list. The function should return a list of nodes in the order they were visited. You can implement this recursively or iteratively.

Visual Example:

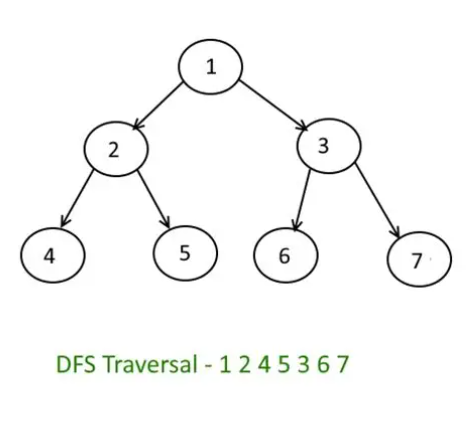
# Using the same graph as before:
graph = {
  'A': ['B', 'C'], 'B': ['A', 'D', 'E'],
  'C': ['A', 'F'], 'D': ['B'],
  'E': ['B', 'F'], 'F': ['C', 'E']
}
# Starting at node 'A'
Input: graph, 'A'
Output: ['A', 'B', 'D', 'E', 'F', 'C']

Note: Other valid DFS paths exist. This one explores A -> B -> D, then backtracks to B and explores B -> E -> F, then backtracks to A and explores A -> C.

Connected Components in a Network

You are given a network of computers represented by an adjacency matrix `isConnected`. If `isConnected[i][j] == 1`, then the `i-th` and `j-th` computers are directly connected. A group of directly or indirectly connected computers is a "component". Return the total number of connected components in the network.

Example:

Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

Data Analysis Question

Analysis of the Iris Dataset

Using a data analysis library like Pandas in Python, perform the following tasks on the Iris dataset.

1. Load Data: Load the Iris dataset from this URL: 'https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv'

2. Grouped Analysis: Group the data by the 'species' column. For each species, calculate and display the average `petal_length`.

3. Filtering: Create a new DataFrame that contains only the `virginica` species whose `sepal_width` is greater than 3.5. Display this new DataFrame.

View Full Python Solutions

BFS Approaches

Approach for Implementing BFS

Use a **queue** data structure (like `collections.deque` in Python) to keep track of nodes to visit.
Use a **set** called `visited` to store nodes that have already been visited to avoid cycles and redundant processing.
Add the `start_node` to the queue and the `visited` set.
Loop while the queue is not empty. In each iteration, dequeue a node.
Process the dequeued node (e.g., add it to your result list).
Iterate through its neighbors. If a neighbor has not been visited, add it to the `visited` set and enqueue it.

Approach for Shortest Path in a Grid

This is a shortest path problem on an unweighted graph, so BFS is the perfect tool.
The "nodes" are the grid cells `(row, col)`.
The queue should store tuples of `(row, col, path_length)`.
Start the queue with `(0, 0, 1)`. Use a `visited` set or modify the grid in-place to mark visited cells.
In the BFS loop, dequeue a cell. If it's the destination `(n-1, n-1)`, return its `path_length`.
Explore all 8 neighbors. For each valid neighbor (within bounds, not an obstacle, and not visited), add it to the queue with `path_length + 1` and mark it as visited.
Handle edge cases: if the start or end cell is an obstacle, no path is possible.

DFS Approaches

Approach for Implementing DFS (Recursive)

Use a **set** `visited` to track visited nodes across recursive calls.
Create a helper function, e.g., `_dfs(node)`.
Inside the helper, first check if the current `node` is already in `visited`. If so, return.
Add the current `node` to the `visited` set and process it (add to result list).
Iterate through the neighbors of the current `node` and make a recursive call `_dfs(neighbor)` for each one.
Start the process by calling the helper function with the `start_node`.

Approach for Connected Components

The goal is to count how many distinct, separate groups of computers exist.
Initialize a `component_count` to 0 and a `visited` set to keep track of computers you've already assigned to a component.
Loop through each computer from `0` to `n-1`.
If the current computer `i` has **not** been visited, it means you've found a new component. Increment `component_count`.
Start a traversal (DFS or BFS) from computer `i`. This traversal will find and mark all other computers connected to `i` by adding them to the `visited` set.
Once the traversal is complete, the loop continues, looking for the next unvisited computer.

Data Analysis Approach

Approach for Iris Dataset Analysis

Load Data: Use the `pandas.read_csv()` function to load the data from the provided URL into a DataFrame.
Grouped Analysis: Use the `.groupby('species')` method on the DataFrame. Then, select the `petal_length` column and apply the `.mean()` aggregation function.
Filtering: Use boolean indexing. Create two conditions: `df['species'] == 'virginica'` and `df['sepal_width'] > 3.5`. Combine these conditions with the `&` (and) operator inside the DataFrame's square brackets `df[...]` to select the desired rows.